上一篇博客里的Dynomite中采用了一个一致性哈希环,所有就去看了一致性哈希算法,下面的内容为对这个算法的一个个人总结
概念
在分布式缓存当中,一致性哈希算法会经常出现,用来解决如何在分布式网络中分布存储和路由这个问题。因为在分布式的环境中存在很多的节点,数据存储在每个节点上,一般的哈希算法在节点变化的过程中会对所有的数据存放都进行重新分配,这将会在资源的耗费上消耗很多。而一致性哈希算法在节点的变化中只会影响到相应节点的数据存储,而不是全部数据,这点就让人非常的开心。
算法描述
现在假设我们所有的缓存节点都是分布在一个环上,这些节点都是根据相应的hash函数计算出在环中的位置的。现在有一些数据需要存储在这些缓存节点当中,那么这些数据是如何选择自己所要的待着的节点呢,也是通过hash函数计算。很明显根据hash函数,节点的计算结果正常来说都不会相同,当然了相同的话也没关系。要是相同的话就直接存储到这个节点上,不同那么就顺时针选择一个离自己最近的一个节点。
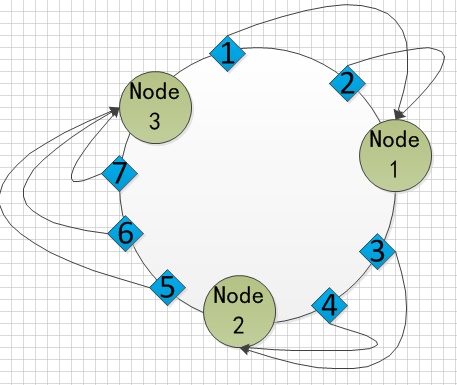
上图所示,这个环上有三个节点,根据hash函数计算出了他们在环上所处的位置,另外存储了七个数据,这七个数据也根据hash函数计算出了他们的位置,那么根据规则:1、2被存储到了Node1节点;3、4被存储到了Node2节点;5、6、7被存储到了Node3节点。这部分的功能其实一般的hash算法都能做到。
下面就看看要是我们这时假设有一个节点故障或者移除了会出现什么情况
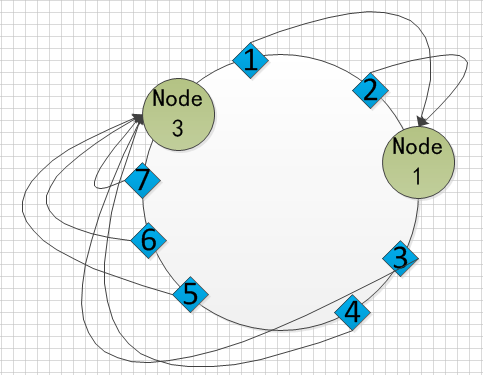
在上图中,我们移除了节点2(Node2),那么它本身因为有数据存储在其中,这里为数据3、4,所有这两个数据需要被转移到别的节点上,根据规则,顺时针寻找离自己最近的节点,它们找到了节点3(Node3),那么数据就存储到Node3上,而其它的数据我们看到存储完全没有变化,也就是说移除节点只跟这个节点上存储的数据有关。同样的,当增加节点时,影响的是从新的节点开始逆时针往上找到的第一个节点之间的数据。
那么下面问题来了,当我们在移除Node2后,3、4的数据全部都存储到了Node3上,而Node1只存储了数据1、2。那么就会出现不平衡的状态,有些节点存储的数据非常多,有些节点又非常的少,一致性hash算法采用了虚拟节点来解决这个问题。也就是说一个实际的物理节点,会复制出若干个虚拟的物理节点,这些虚拟节点的位置和物理节点不相同,也是根据hash函数计算后分布在这个环上的,但是虚拟毕竟是虚拟,所有的数据实际上是存储在物理节点上的。
上图中,Node1-2为物理节点Node1-1的虚拟节点;Node3-2为Node3-1的虚拟节点,这样就会有效的防止某个物理节点上存储的数据过多,而某些节点存储数据过少这种情况。
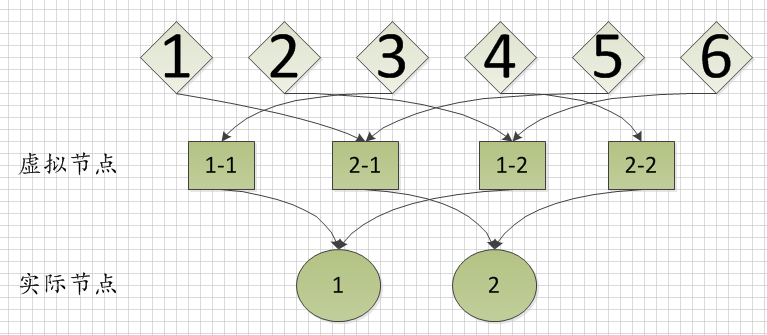
上图中,我们有实际节点1、2;根据实际节点虚拟出来的虚拟节点1-1、2-1、1-2、2-2;需要存储的数据1、2、3、4、5、6;
假设现在数据1、5是存储在节点2-1中;数据2、6是存储在1-2中;数据3存储在1-1;数据4存储在2-2;所以实际数据存储情况为,数据2、3、6存储在物理节点1中,1、4、5存储在物理节点2中。每个物理节点虚拟出来的虚拟节点个数可以根据实际情况来选择。
代码
下面是取自groupcache中实现的一致性hash代码中,我做了部分修改。
package main
import (
"fmt"
"hash/crc32"
"sort"
"strconv"
)
type Hash func(data []byte) uint32
type Map struct {
hash Hash
replicas int
keys []int // Sorted
hashMap map[int]string
}
func New(replicas int, fn Hash) *Map {
m := &Map{
replicas: replicas,
hash: fn,
hashMap: make(map[int]string),
}
if m.hash == nil {
m.hash = crc32.ChecksumIEEE
}
return m
}
// Returns true if there are no items available.
func (m *Map) IsEmpty() bool {
return len(m.keys) == 0
}
// Adds some keys to the hash.
func (m *Map) Add(keys ...string) {
for _, key := range keys {
for i := 0; i < m.replicas; i++ {
hash := int(m.hash([]byte(strconv.Itoa(i) + key)))
m.keys = append(m.keys, hash)
m.hashMap[hash] = key
}
}
sort.Ints(m.keys)
}
// Gets the closest item in the hash to the provided key.
func (m *Map) Get(key string) string {
if m.IsEmpty() {
return ""
}
hash := int(m.hash([]byte(key)))
// Binary search for appropriate replica.
idx := sort.Search(len(m.keys), func(i int) bool { return m.keys[i] >= hash })
// Means we have cycled back to the first replica.
if idx == len(m.keys) {
idx = 0
}
return m.hashMap[m.keys[idx]]
}
func (m *Map) Del(key string) {
if m.IsEmpty() {
return
}
var hash uint32
for i := 0; i < m.replicas; i++ {
//log.Fatal("not panic:", i)
hash = m.hash([]byte(strconv.Itoa(i) + key))
// fmt.Println(m.hashMap)
delete(m.hashMap, int(hash))
// fmt.Println(m.hashMap)
// fmt.Println(m.keys)
ids := sort.Search(len(m.keys), func(i int) bool {
//fmt.Printf("m.keys[%d]:%d-->hash:%d\n", i, m.keys[i], int(hash))
return m.keys[i] >= int(hash)
})
copy(m.keys[ids:], m.keys[ids+1:])
m.keys = m.keys[:len(m.keys)-1]
}
}
func main() {
ring := New(3, nil)
ring.Add("zkkk", "fanp", "lixm", "ppoo", "weir", "zhgk")
for i := 0; i < 20; i++ {
str := fmt.Sprintf("James.km%03d", i)
name := ring.Get(str)
fmt.Printf("[%16s] is in node: [%16s]\n", str, name)
}
ring.Add("zouq")
fmt.Println("after add new node")
for i := 0; i < 20; i++ {
str := fmt.Sprintf("James.km%03d", i)
name := ring.Get(str)
fmt.Printf("[%16s] is in node: [%16s]\n", str, name)
}
ring.Del("zouq")
fmt.Println("after delete zouq node")
for i := 0; i < 20; i++ {
str := fmt.Sprintf("James.km%03d", i)
name := ring.Get(str)
fmt.Printf("[%16s] is in node: [%16s]\n", str, name)
}
}