用go语言实现的一个简单的treap

Treap的简单介绍

顾名思义，Treap=Tree+Heap。这里引用NOCOW里的一句话描述：Treap，就是有另一个随机数满足堆的性质的二叉搜索树，其结构相当于以随机顺序插入的二叉搜索树。其基本操作的期望复杂度为O(log n)。其特点是实现简单，效率高于伸展树并且支持大部分基本功能，性价比很高。更加详细的描述可以去维基百科上查阅。 没错，它实现起来相对于红黑树或者AVL树来说确实没那么的复杂，下面就实现一个go语言的版本。

代码部分

由于Treap=Tree+Heap，所以树和堆的特点，它兼而有之。根据上面的定义，我们需要一个随机数来满足堆的性质，下面看看节点的定义代码

type Node struct {
        data       int
        priority   int64
        leftChild  *Node
        rightChild *Node
    }

结构体中的priority就是一个存储优先级的变量。有了节点的结构定义，下面就要创建这个节点

/*创建节点*/
    func NewBSTNode(x int) (node *Node) {
        node = &Node{
            data:       x,
            priority:   rand.Int63(),
            leftChild:  nil,
            rightChild: nil,
        }
        return
    }

由于它的值是一个随机数，所以我们这里采用rand.Int63()来生成它。它除了优先级之外还有一个存储数据的变量data，还有一个左子树leftChild跟右子树rightChild,除了这个优先级的变量定义之外和一般的二叉树定义没有什么区别。为了理解起来方便，在代码中又定义了一个创建树的函数

/*创建一课BST树*/
    func NewBST() *Node {
        return nil
    }

函数里面什么也没做，只是简单的返回了一个nil。

有了树有了节点，那就要把节点插入到树中

func Insert(t, node *Node) *Node {
        if t == nil {
            t = node
        } else if t.data > node.data {
            t.leftChild = Insert(t.leftChild, node)
            if t.priority > node.priority {
                t = rightRotato(t)
            }
        } else {
            t.rightChild = Insert(t.rightChild, node)
            if t.priority > node.priority {
                t = leftRotato(t)
            }
        }
        return t
    }

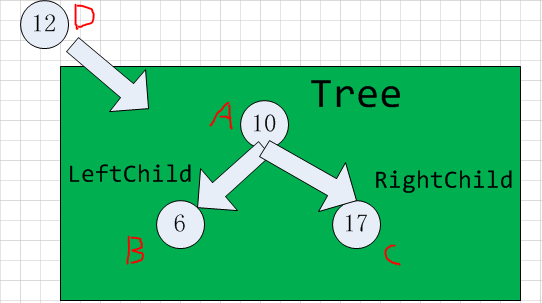
首先判断这棵树是否为nil，若是则直接把node赋给t，返回。
若不为nil则判断待插入的节点的数据域

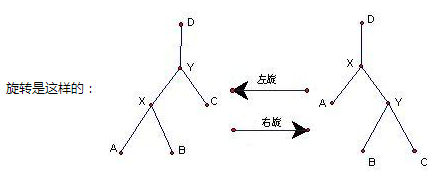
若D.data>A.data,则D插入到左子树，否则插入右子树。这个插入操作是递归实现的。到目前为止，所有的操作跟一般的二叉查找树没有区别。接下去Treap还会比较优先级，为了维护堆性质，根据优先级修改之前插入好的二叉查找树，修改是通过旋转来实现的。有左旋转和右旋转。

先看左旋转代码

/*左旋转*/
    func leftRotato(p *Node) *Node {
        b := p.rightChild
        p.rightChild = b.leftChild
        b.leftChild = p
        return b
    }

p为当前子树的根节点，旋转的前提是，插入的子节点的priority比根节点的小，不符合堆性质，所以旋转，旋转的目前是让p和子节点根据规定交换位置，这个规定就是不能破坏二叉查找树的性质。代码中，首先保存了p的右子树到b，b就是一个子节点。由于这个旋转是由下自上进行的，所以在进行到b的时候，以它为根节点的树是符合性质的。因为b的左子树中节点的data肯定比p的data大，所以将b的左子树赋给p的右子树(p.rightChild = b.leftChild)，然后把p赋给b的左子树(b.leftChild = p)，现在b就是这棵子树的根节点，一次左旋转完成。

右旋转代码

/*右旋转*/
    func rightRotato(p *Node) *Node {
        b := p.leftChild
        p.leftChild = b.rightChild
        b.rightChild = p
        return b
    }

右旋转的方式跟左旋转一样，只是换了一个方向而已。

这里关键点为，当我们插入一个新节点的时候，在未旋转之前，这个节点肯定是插入到页节点上，并成为一个新的页节点，在插入之后判断是否需要旋转，若需要旋转，这个旋转肯定是从刚插入的父节点为根节点的子树开始做旋转操作的。

遍历

在建立了一棵treap树之后，查找数据就需要用到遍历的方法，遍历分为中序，前序，后序。

//中序遍历
    func (node *Node) midPrint() {
        if node != nil {
            node.leftChild.midPrint()
            fmt.Println(node.data, node.priority)
            node.rightChild.midPrint()
        }
    }

前序和后序的方法差不多，只是打印节点值的位置不一样。

可能有些地方描述的还不是很清楚。关键是这个旋转，这里的旋转比红黑树的旋转要简单的多。

非专业娱乐型程序员。
Published under (CC) BY-NC-SA in categories 技术 tagged with golang 数据结构
2014-11-17